Des méthodes de calcul asymptotiques permettant de couvrir une large variété de situations ont été développées. On caractérise habituellement l’état de surface par 3 paramètres :
- La rugosité intrinsèque fonction du ratio entre l’écart type de la hauteur des rugosités par rapport au plan moyen à la longueur d’onde,
- La pente définie comme le ratio de l’écart type précédent à la distance d’autocorrélation,
- La fonction d’autocorrélation.
Trois familles de modèles ont été développées permettant de traiter différents cas possibles:
- Faiblement rugueux : la technique des faibles pentes, y compris les problèmes double échelle
- Rugosités moyennes et fortes : l’algorithme utilise l’approximation de Kirchhoff
- Très fortement rugueux : l’algorithme utilise l’approximation de Kirchhoff à l’ordre 2
 |
 |
|
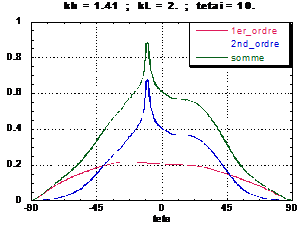
Indicatrice de diffusion
Approximation de Kirchhoff 1er et 2nd ordre
|
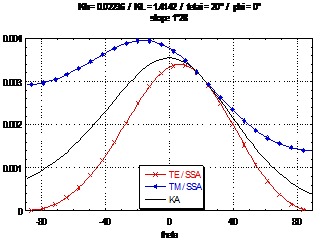
Indicatrice de diffusion
Méthode des faibles pentes (SSA)
comparée à l’approximation de Kirchhoff
|
Références
(les textes complets sont disponibles dans la section publications)
Y. Beniguel, G. Berginc, "Une revue des techniques utilisees pour le calcul de la diffraction par les surfaces rugueuses aleatoires", Journees d'etudes sur la propagation electromagnetique dans l'atmosphere : du decametrique a l'angstrom, Rennes, 2002.
G. Berginc, Y. Beniguel, B. Chevalier, "Small slope approximation method : Higher order contributions for scattering from conducting 3D surfaces", SPIE99 Proceedings, Denver, 1999.










